Um número natural é denominado “número primo” quando apresenta apenas dois divisores naturais: ele mesmo e o número 1. Existem infinitos números primos. A seguir indicamos os números primos menores que 100.


OBS: Números Primos entre si
Dois números naturais são denominados “números primos entre si” quando apresentam como único divisor comum o número 1.
Exemplo: 15 e 16

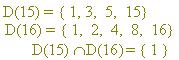D( N ) = conjunto de divisores de N
III – M.M.C E M.D.C
A utilização de mmc e mdc nas resoluções de problemas é muito comum já que um trata de múltiplos e o outro de divisores comuns de dois ou mais números. Antes de estudarmos as aplicações vejamos como obtê-los.
MAXIMO DIVISOR COMUM  ( M.D.C )
O máximo divisor comum (mdc) entre dois números naturais é obtido a partir da interseção dos divisores naturais, escolhendo-se a maior. O mdc pode ser calculado pelo produto dos fatores primos que são comuns tomando-se sempre o de menor expoente.
Exemplo: 120 e 36



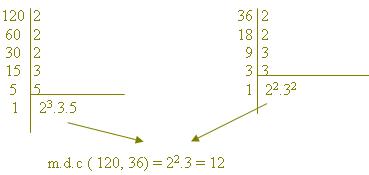
OBS: O m.d.c pode ser calculado pela decomposição simultânea em fatores primos, tomando apenas os fatores que dividem simultaneamente.



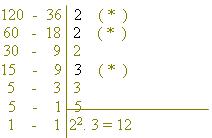
MÍNIMO MÚLTIPLO COMUM (M.M.C)
O número múltiplo comum entre dois números naturais é obtido a partir da interseção dos múltiplos naturais, escolhendo-se o menor excetuando o zero. O m.m.c pode ser calculado pelo produto de todos os fatores primos, considerados uma única vez e de maior expoente.
Exemplo: 120 e 36



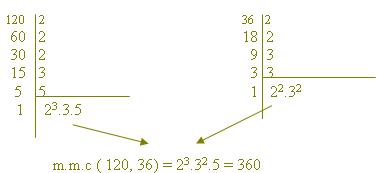
OBS: O m.m.c pode ser calculado pela decomposição simultânea em fatores primos.


OBS : Existe uma relação entre o m.m.c e o m.d.c de dois números naturais a e b
m.m.c.(a,b) . m.d.c. (a,b) = a . b
O produto entre o m.m.c e m.d.c de dois números é igual ao produto entre os dois números.
Em uma divisão existem alguns termos: dividendo (número que será dividido) quociente (resultado da divisão), divisor (número que divide) e resto (o que sobra da divisão), quando o resto é igual a zero dizemos que a divisão é exata. Sendo assim, podemos concluir que nessa divisão ocorre uma divisibilidade, ou seja, podemos encontrar múltiplos e divisores.
Por exemplo, quando resolvemos a divisão 123 : 3 encontramos como quociente 41 e resto igual a 0.
Concluímos que essa divisão é exata (não sobra resto maior que zero), então dizemos que:
123 é divisível por 3, pois a divisão é exata; ou que 123 é múltiplo de 3, pois existe um número natural que multiplicado por 3 resulta em 123; ou que 3 é divisor de 123, pois existe um número que divide 123 e resulta em 3.
A partir desse exemplo podemos definir múltiplo e divisor como:
Múltiplos são resultados de uma multiplicação de dois números naturais. Por exemplo, 30 é múltiplo de 6, pois 6 x 5 = 30.
Divisores são números que dividem outros, desde que a divisão seja exata, por exemplo: 2 é divisor de 10, pois
10: 2 = 5.
Quando especificamos os múltiplos e os divisores de um número formamos conjuntos dos múltiplos e dos divisores, veja alguns exemplos de conjunto dos múltiplos e divisores de números naturais e perceba as suas particularidades.
M(5) = {0,5,10,15,20,25,30,35, ... }
M(15) = {0,15,30,45,60,75, ... }
M(10) = {0,10,20,30,40,50,60, ... }
M(2) = {0,2,4,6,8,10,12,14,16, ...}
Observando os conjuntos acima percebemos que todos eles são infinitos e que possuem um elemento em comum, o elemento 0. Como todos os conjuntos citados são formados por múltiplos de números, podemos concluir que o conjunto dos múltiplos de qualquer número sempre será infinito, pois existem infinitos números naturais que podem ser multiplicados. Podemos concluir também que sempre o 0 fará parte dos elementos de um conjuntos dos múltiplos de um número, pois qualquer número multiplicado por zero resultará em zero.
D(55) = {1,5,11,55}
D(10) = {1,2,5,10}
D(20) = {1,2,4,5,10,20}
D(200) = {1,2,4,5,8,10,20,40,50,100,200}
Os conjuntos dos divisores de números naturais deixam claro que todos esses conjuntos são finitos, pois não é toda divisão que o resto é igual a zero e o número 1 é divisor de qualquer número natural, pois qualquer número dividido por ele mesmo é igual a 1.
OBSERVAÇÕES:
• Quando um número é divisível por apenas um e por ele mesmo dizemos que esse número é primo.
• O único número primo par é o 2.
POTENCIAÇÃO
Consideremos uma multiplicação em que todos os fatores são iguais
Exemplo
5x5x5, indicada por 5³
ou seja , 5³= 5x5x5=125
onde :
5 é a base (fator que se repete)
3 é o expoente ( o número de vezes que repetimos a base)
125 é a potência ( resultado da operação)
a) 7²=
b) 4³=
 O expoente 2 é chamado de quadrado
O expoente 3 é chamado de cubo
O expoente 4 é chamado de quarta potência.
O expoente 5 é chamado de quinta potência.

a) 7² Lê-se:
b) 4³ Lê-se:
c) 5 4Lê-se:
d) 2 5 Lê-se:

Por convenção temos que:
1) todo o número elevado ao expoente 1 é igual à própria base,
a) 8¹ =
b) 5¹ =
c) 15¹ =

2) todo o número elevado ao expoente zero é igual a 1
exemplo
a) 8º=
b) 4º=
c) 12º=

1) Em 7² = 49, responda:
a) Qual é a base?
b) Qual é o expoente?
c) Qual é a potência?

2) Escreva na forma de potência:
a) 4x4x4=
b) 5x5 =
c) 9x9x9x9x9= 
d) 7x7x7x7 =
e) 2x2x2x2x2x2x2=

3) Calcule a potência:
a) 3² =
b) 8² =
c) 2³=
d) 3³ =
e) 6³ =
m) 10² =
n) 10³ =
o) 15² =
p) 17² =
q) 30² =
m) 10² =
n) 10³ =
o) 15² =
p) 17² =
q) 30² =

4) Calcule as potências:
a)40² =
b)32² =
c)15³ =
d) 30³=
e) 11⁴ =
f) 300² =
g) 100³ =
h) 101² =

5) Calcule as Potências:
a) 11² =
b) 20² =
c) 17² =
d) 0² =
e) 0¹ =
g) 10³ =
h) 470¹ =
i) 11³ =
jn) 15³ =
o) 1² =
Para resolver uma expressão numérica, efetuamos as operações obedecendo à seguinte ordem :
1°) Potenciação
2°) Multiplicações e divisões
3°) Adições e Subtrações
EXEMPLOS
1) exemplo
   5 + 3² x 2 =
= 5 + 9 x 2 =
= 5 + 18 =
= 23

2) exemplo
 7² - 4 x 2 + 3 =
= 49 – 8 + 3 =
= 41 + 3 =
= 44
Há expressões onde aparecem os sinais de associação e que devem ser eliminados nesta ordem:
1°) parênteses ( )
2°) colchetes [ ]
3°) chaves { }
exemplos
1°) exemplo

   40 – [5² + ( 2³ - 7 )] =
= 40 – [5² + ( 8 - 7 )]
= 40 – [25 + 1 ]=
= 40 – 26 =
= 14

2°) exemplo

   50 –{ 15 + [ 4² : ( 10 – 2 ) + 5 x 2 ] } =
= 50 –{ 15 + [ 16 : 8 + 10 ]}=
= 50 – { 15 + [ 2 + 10 ] } =
= 50 – { 15 +12 } =
= 50 – 27 =
= 23

Exercícios

1) Calcule o valor das expressões:
a) 7² - 4 =
b) 2³ + 10 =
c) 5² - 6 =
g) 10³ - 10² =
i) 5² - 3² =

2) Calcule
a) 3² + 5 =
b) 3 + 5² =
c) 3² + 5² =
d) 5² - 3² =
f) 5³ - 2² =
g) 10 + 10² =
h) 10³ - 10² =
i) 10³ - 1¹ =

3) Calcule o valor das expressões
a) 2³ x 5 + 3² =
e) 5² + 3 x 2 – 4 =
f) 5 x 2² + 3 – 8 =
g) 5² - 3 x 2² - 1 =
h) 16 : 2 – 1 + 7² =

4) calcule o valor das expressões:
a) 5² : ( 5 +1 -1)+ 4 x 2 =
c) 3²: ( 4 – 1) + 3 x 2² =
d) 70 –[ 5 x (2² : 4) + 3²] =
e) ( 7 + 4) x ( 3² - 2³) =
f) 5² + 2³ - 2 x (3 + 9) =
g) 6² : 3² + 4 x 10 – 12 =
h) (7² - 1 ) : 3 + 2 x 5 =

5) calcule o valor das expressões:
a) 5 + 4²- 1 =
d) 10²- 3² + 5 =
e) 11² - 3² + 5 =
f) 5 x 3² x 4 =
g) 5 x 2³ + 4² =
h) 5³ x 2² - 12 =

6) Calcule o valor das expressões:
a) ( 4 + 3)² - 1 =
b) ( 5 + 1 )² + 10 =
c) ( 9 – 7 )³ x 8 =
d) ( 7² - 5²) + ( 5² - 3 ) =
f) 3² x 2³ + 2² x 5² =

7) Calcule o valor das expressões:
a) 4²- 10 + (2³ - 5) =
b) 30 – (2 + 1)²+ 2³ =
c) 30 + [6² : ( 5 – 3) + 1 ] =
d) 20 – [6 – 4 x( 10 - 3²) + 1] =
e) 50 + [ 3³ : ( 1 + 2) + 4 x 3] =
g) [ 4² + ( 5 – 3)³] : ( 9 – 7)³ =
h) 7²+ 2 x[(3 + 1)² - 4 x 1³] =
i) 25 + { 3³ : 9 +[ 3² x 5 – 3 x (2³- 5¹)]} =

8) Calcule as expressões:
b) ( 3² - 2³) . 3³ - 2³ + 2² . 4² =
d) [2 . (10 - 4² : 2) + 6²] : ( 2³ - 2²) =
h) 13 + ( 10 – 8 + (7 – 4)) =
i) (10 . 4 + 18 – ( 2 . 3 +6)) =
j) 7 . ( 74 – ( 4 + 7 . 10)) =
k) ( 19 : ( 5 + 3 . 8 – 10)) =
RADICIAÇÃO
Qual o número que elevado ao quadrado é igual a 9?
Solução
Sendo 3² = 9, podemos escrever que √9 = 3
Essa operação chama-se radiciação, que é a operação inversa da potenciação
Potenciação------------------------radiciação
a) 7² = 49 ---------------------------- √
b) 2³= 8 ------------------------------ √
O sinal √ chamamos de radical
O índice 2 significa : raiz quadrada
O índice 3 significa: raiz cúbica
O índice 4 significa: raiz quarta

√49= 7 lê-se:
Nota:
Não é necessário o índice 2 no radical para a raiz quadrada

1)Descubra o número que :
a) elevado ao quadrado dá 9
b) elevado ao quadrado dá 25
c) elevado ao quadrado dá 49
d) elevado ao cubo dá 8

3) Determine a Raiz quadrada:
a) √9 =
b) √16 =
c) √25 =
d) √81 =
e) √0 =
f) √1 =
g) √64 =
h) √100 =

4) Resolva as expressões abaixo:
a) √16 + √36 = 4 + 6 =
b) √25 + √9 = 5 + 3 =
c) √49 - √4 = 7 - 2 =
d) √36- √1 = 6 - 1 =
e) √9 + √100 = 3 + 10 =
f) √4 x √9 = 2 x 3 =
MULTIPLOS E DIVISORES
Os múltiplos e divisores de um número estão relacionados entre si da seguinte forma:
Se 15 é divisível por 3, então 3 é divisor de 15, assim, 15 é múltiplo de 3.
Se 8 é divisível por 2, então 2 é divisor de 8, assim, 8 é múltiplo de 2.
Se 20 é divisível por 5, então 5 é divisor de 20, assim, 20 é múltiplo de 5.
Múltiplos de um número natural
Denominamos múltiplo de um número o produto desse número por um número natural qualquer. Um bom exemplo de números múltiplos é encontrado na tradicional tabuada.
Múltiplos de 2 (tabuada da multiplicação do número 2)
2 x 0 = 0
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
2 x 5 = 10
2 x 6 = 12
2 x 7 = 14
2 x 8 = 16
2 x 9 = 18
2 x 10 = 20
É assim sucessivamente.
Múltiplos de 3 (tabuada da multiplicação do número 3)
3 x 0 = 0
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
3 x 5 = 15
3 x 6 = 18
3 x 7 = 21
3 x 8 = 24
3 x 9 = 27
3 x 10 = 30
É assim sucessivamente.
Portanto, os múltiplo de 2 são: 0, 2, 4, 6, 8, 10, 12, 14, 18, 20, ...
E os múltiplos de 3 são: 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, ...
Observe que os múltiplos do número escolhido obedecem a uma progressão aritmética com razão igual ao múltiplo estabelecido. Nos múltiplos de 2 a razão é 2, nos múltiplos de 3 a razão é 3 e assim sucessivamente. Veja mais exemplos:
Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, ...
Múltiplos de 5: 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, ...
Divisores de um número natural
Um número é divisor de outro quando o resto da divisão for igual a 0. Portanto,
12 é divisível por 1, 2, 3, 4, 6 e 12.
36 é divisível por 1, 2, 3, 4, 6, 9, 12, 18 e 36.
48 é divisível por 1, 2, 3, 4, 6, 8, 12, 24 e 48.
Observações importantes:
Ø O menor divisor natural de um número é sempre o número 1.
Ø O maior divisor de um número é o próprio número.
Ø O zero não é divisor de nenhum número.
Ø Os divisores de um número formam um conjunto finito.
Alguns números têm apenas dois divisores: o 1 e ele mesmo. Esses números são chamados de primos. Observe os números primos de 1 a 100 destacados no crivo de Eratóstenes:



Em uma divisão existem alguns termos: dividendo (número que será dividido) quociente (resultado da divisão), divisor (número que divide) e resto (o que sobra da divisão), quando o resto é igual a zero dizemos que a divisão é exata. Sendo assim, podemos concluir que nessa divisão ocorre uma divisibilidade, ou seja, podemos encontrar múltiplos e divisores.
Por exemplo, quando resolvemos a divisão 123 : 3 encontramos como quociente 41 e resto igual a 0.
Concluímos que essa divisão é exata (não sobra resto maior que zero), então dizemos que:
123 é divisível por 3, pois a divisão é exata; ou que 123 é múltiplo de 3, pois existe um número natural que multiplicado por 3 resulta em 123; ou que 3 é divisor de 123, pois existe um número que divide 123 e resulta em 3.
A partir desse exemplo podemos definir múltiplo e divisor como:
Múltiplos são resultados de uma multiplicação de dois números naturais. Por exemplo, 30 é múltiplo de 6, pois 6 x 5 = 30.
Divisores são números que dividem outros, desde que a divisão seja exata, por exemplo: 2 é divisor de 10, pois
10: 2 = 5.
Quando especificamos os múltiplos e os divisores de um número formamos conjuntos dos múltiplos e dos divisores, veja alguns exemplos de conjunto dos múltiplos e divisores de números naturais e perceba as suas particularidades.
M(15) = {0,15,30,45,60,75, ... }
M(10) = {0,10,20,30,40,50,60, ... }

Observando os conjuntos acima percebemos que todos eles são infinitos e que possuem um elemento em comum, o elemento 0. Como todos os conjuntos citados são formados por múltiplos de números, podemos concluir que o conjunto dos múltiplos de qualquer número sempre será infinito, pois existem infinitos números naturais que podem ser multiplicados. Podemos concluir também que sempre o 0 fará parte dos elementos de um conjuntos dos múltiplos de um número, pois qualquer número multiplicado por zero resultará em zero.
D(55) = {1,5,11,55}
D(10) = {1,2,5,10}
D(20) = {1,2,4,5,10,20}
D(200) = {1,2,4,5,8,10,20,40,50,100,200}
Os conjuntos dos divisores de números naturais deixam claro que todos esses conjuntos são finitos, pois não é toda divisão que o resto é igual a zero e o número 1 é divisor de qualquer número natural, pois qualquer número dividido por ele mesmo é igual a 1.
OBSERVAÇÕES:
• Quando um número é divisível por apenas um e por ele mesmo dizemos que esse número é primo.
• O único número primo par é o 2.
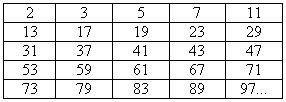
Um número natural é denominado “número primo” quando apresenta apenas dois divisores naturais: ele mesmo e o número 1. Existem infinitos números primos. A seguir indicamos os números primos menores que 100.

OBS: Números Primos entre si
Dois números naturais são denominados “números primos entre si” quando apresentam como único divisor comum o número 1.
Exemplo: 15 e 16


D( N ) = conjunto de divisores de N
III – M.M.C E M.D.C
A utilização de mmc e mdc nas resoluções de problemas é muito comum já que um trata de múltiplos e o outro de divisores comuns de dois ou mais números. Antes de estudarmos as aplicações vejamos como obtê-los.
 MAXIMO DIVISOR COMUM  ( M.D.C )
O máximo divisor comum (mdc) entre dois números naturais é obtido a partir da interseção dos divisores naturais, escolhendo-se a maior. O mdc pode ser calculado pelo produto dos fatores primos que são comuns tomando-se sempre o de menor expoente.
Exemplo: 120 e 36
OBS: O m.d.c pode ser calculado pela decomposição simultânea em fatores primos, tomando apenas os fatores que dividem simultaneamente.
MÍNIMO MÚLTIPLO COMUM (M.M.C)
O número múltiplo comum entre dois números naturais é obtido a partir da interseção dos múltiplos naturais, escolhendo-se o menor excetuando o zero. O m.m.c pode ser calculado pelo produto de todos os fatores primos, considerados uma única vez e de maior expoente.
Exemplo: 120 e 36
OBS: O m.m.c pode ser calculado pela decomposição simultânea em fatores primos.
OBS : Existe uma relação entre o m.m.c e o m.d.c de dois números naturais a e b
m.m.c.(a,b) . m.d.c. (a,b) = a . b
O produto entre o m.m.c e m.d.c de dois números é igual ao produto entre os dois números.